- Home
- Antike
- Geometrie
- Logik
- Gallery
- Literatur
- Studium
- Surface Theory
Theorem zu den definitionen 3, 4 und 5
Bedeutung der
Theoreme
Darstellung der Theoreme
Es seien \( a\in{\mathcal P} \) und \( k\in{\mathcal F}. \) Dann gilt \[ (x\in ak)\longleftrightarrow(x\in{\mathcal P}\ \mbox{und es gibt ein}\ y\in k\ \mbox{mit}\ x\in ay). \]

Dieses Theorem spielt eine zu Theorem 1 vergleichbare Rolle. Sein Beweis ergibt sich unmittelbar aus Definition 3 der geometrischen Figur \( ak. \)
|
Beweis |
|
|
Es sei \( x\in ak. \) |
|
|
1. |
\( \vdash\ x\in{\mathcal P} \) |
|
2. |
\( \vdash\ \exists\,y\in k\,(x\in ay) \) |
|
Es sei \( x\in{\mathcal P}, \) und es existiere ein \( y\in k \) mit \( x\in ay. \) |
|
|
3. |
\( \vdash\ x\in ak \) |
|
Damit ist die Behauptung bewiesen. \( \quad\Box \) |
|
Es seien \( a\in{\mathcal P} \) und \( k\in{\mathcal F}. \) Dann gilt \[ (x\in ak)\longleftrightarrow(x\in{\mathcal P}\ \mbox{und es gilt}\ k\cap a'x\not=\emptyset). \]
Zur Veranschaulichung dieser Aussage verweisen wir auf voriges Bild zu Theorem 5.
|
Beweis: |
||
|
Es sei \( x\in ak \) |
||
|
1. |
Es ist \( x\in{\mathcal P} \) |
(Th 5) |
|
2. |
Es existiert ein \( y\in k \) mit \( x\in ay \) |
(Th 5) |
|
3. |
Es existiert ein \( y\in k \) mit \( y\in\{z\in{\mathcal P}\,:\,x\in az\} \) |
(2) |
|
4. |
Es existiert ein \( y\in k \) mit \( y\in a'x \) |
(3, Def 1) |
|
5. |
Es sind \( x\in{\mathcal P} \) und \( k\cap a'x\not=\emptyset \) |
(1, 4) |
|
Es seien \( x\in{\mathcal P} \) und \( k\cap a'x\not=\emptyset \) |
||
|
6. |
Es existiert ein \( y\in k\cap a'x \) |
|
|
7. |
Es existiert ein \( y\in k \) mit \( y\in a'x \) |
(6) |
|
8. |
Es existiert ein \( y\in k \) mit \( y\in\{z\in{\mathcal P}\,:\,x\in az\} \) |
(7, Def 1) |
|
9. |
Es existiert ein \( y\in k \) mit \( x\in ay \) |
(8) |
|
10. |
Es ist \( x\in\{z\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ z\in ak\} \) |
(9) |
|
11. |
Es ist \( x\in ak \) |
(10, Def 1) |
|
Damit ist der Beweis abgeschlossen.\( \quad\Box \) |
||
Es seien \( a\in{\mathcal P} \) und \( k\in{\mathcal F}. \) Dann gilt \[ (x\in a'k)\longleftrightarrow(x\in{\mathcal P}\ \mbox{und es gilt}\ k\cap ax\not=\emptyset). \]

Ein beliebig gewählter \( x \) der geometrischen Figur \( a'k \) erzeugt mit dem Punkt \( a \) eine Figur \( ax, \) welche mit der Figur \( k \) einen nicht leeren Durchschnitt
besitzt.
| Beweis: | ||
|
Es sei \( x\in a'k \) |
||
|
1. |
Es ist \( x\in{\mathcal P} \) |
(Def 4) |
|
2. |
Es existiert ein \( z\in k \) mit \( x\in a'z \) |
(Def 4) |
|
3. |
Es existiert ein \( z\in k \) mit \( z\in ax \) |
(2, Def 1) |
|
4. |
Es ist \( k\cap ax \not=\emptyset \) |
(3) |
|
Es sei \( x\in{\mathcal P}, \) und es gelte \( k\cap ax\not=\emptyset \) |
||
|
5. |
Es existiert ein \( z\in k \) mit \( z\in ax \) |
|
|
6. |
Es existiert ein \( z\in k \) mit \( x\in\{w\in{\mathcal P}\,:\,z\in aw \} \) |
(5) |
|
7. |
Es existiert ein \( z\in k \) mit \( x\in a'z \) |
(6, Def 1) |
|
8. |
Es ist \( x\in\{y\in{\mathcal P}\,:\,\mbox{es gibt ein}\ z\in k\ \mbox{mit}\ y\in a'z \} \) |
(7) |
|
9. |
Es ist \( x\in a'k \) |
(8, Def 4) |
|
Damit ist der Beweis abgeschlossen. \( \quad\Box \) |
||
Es seien \( a\in{\mathcal P} \) und \( k\in{\mathcal F}. \) Dann gilt \[ (x\in ak')\longleftrightarrow(x\in{\mathcal P}\ \mbox{und es gilt}\ k\cap x'a\not=\emptyset). \]

Ein beliebig gewählter Punkt \( x \) der geometrischen Figur \( ak' \) erzeugt mit dem Punkt \( a \) eine Figur \( x'a, \) welche mit der Figur \( k \) einen nicht leeren Durchschnitt
besitzt.
| Beweis: | ||
|
Es sei \( x\in ak'. \) Wir zeigen \( x\in{\mathcal P} \) und \( k\cap x'a\not=\emptyset. \) |
||
|
1. |
Es ist \( x\in{\mathcal P} \) |
(Def 5) |
|
2. |
Es existiert ein \( z\in k \) mit \( x\in az' \) |
(Def 5) |
|
3. |
Es existiert ein \( z\in k \) mit \( a\in xz \) |
(2, Th 3) |
|
4. |
Es existiert ein \( z\in k \) mit \( z\in x'a \) |
(3, Th 2) |
|
5. |
Es sind \( x\in{\mathcal P} \) und \( k\cap x'a\not=\emptyset \) |
(1, 4) |
|
Es sei \( x\in{\mathcal P}, \) und es gelte \( k\cap x'a\not=\emptyset. \) Wir zeigen \( x\in ak'. \) |
||
|
6. |
Es existiert ein \( z\in k \) mit \( z\in x'a \) |
|
|
7. |
Es existiert ein \( z\in k \) mit \( a\in xz \) |
(6, Th 2) |
|
8. |
Es existiert ein \( z\in k \) mit \( x\in az' \) |
(7, Th 3) |
|
9. |
Es ist \( x\in\{y\in{\mathcal P}\,:\,\mbox{es gibt ein}\ z\in k\ \mbox{mit}\ y\in az'\} \) |
(8) |
|
10. |
Es ist \( x\in ak' \) |
(9, Def 5) |
|
Damit ist der Beweis abgeschlossen. \( \quad\Box \) |
||
Es seien \( a,b\in{\mathcal P} \) und \( k\in{\mathcal F}. \) Dann gilt \[ (b\in ak)\longleftrightarrow(a\in bk'). \]

| Beweis: | ||
|
Es sei \( b\in ak. \) Wir zeigen \( a\in bk'. \) |
||
|
1. |
Es ist \( b\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in ay\} \) |
(Def 3) |
|
2. |
Es gibt ein \( y\in k \) mit \( b\in ay \) |
(1) |
|
3. |
Es gibt ein \( y\in k \) mit \( a\in by' \) |
(2, Th 2) |
|
4. |
Es ist \( a\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in by'\} \) |
(3) |
|
5 |
Es ist \( a\in bk' \) |
(4, Def 5) |
|
Es sei \( a\in bk'. \) Wir zeigen \( b\in ak. \) |
||
|
6. |
Es ist \( a\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in by'\} \) |
(Def 5) |
|
7. |
Es gibt ein \( y\in k \) mit \( a\in by' \) |
(6) |
|
8. |
Es gibt ein \( y\in k \) mit \( b\in ay \) |
(7, Th 3) |
|
9. |
Es ist \( b\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in ay\} \) |
(8) |
|
10. |
Es ist \( b\in ak \) |
(9, Def 3) |
|
Damit ist der Beweis abgeschlossen. \( \quad\Box \) |
||
Es seien \( a\in{\mathcal P} \) und \( h,k\in{\mathcal F}. \) Dann gilt \[ (h\subseteq k)\longrightarrow(ah\subseteq ak). \]

Sind \( a \) ein beliebiger Punkt und \( h\) sowie \( k \) zwei geometrische Figuren, wobei \( h \) in \( k \) enthalten ist, so ist auch \( ah \) enthalten in \( ak. \)
| Beweis: | ||
|
Nach Voraussetzung ist \( h\subseteq k. \) |
||
|
1. |
Falls \( y\in h, \) so ist \( y\in k \) |
(Vor) |
|
Es sei \( z\in ah \) beliebig. Wir zeigen \( z\in ak \). |
||
|
2. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\ \mbox{mit}\ x\in ay\} \) |
(Def 3) |
|
3. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in ay\} \) |
(1, 2) |
|
4. |
Es ist \( z\in ak \) |
(3, Def 3) |
|
Damit ist der Beweis abgeschlossen. \( \quad\Box \) |
||
Es seien \( a\in{\mathcal P} \) und \( h,k\in{\mathcal F}. \) Dann gilt \[ (h\subseteq k)\longrightarrow(a'h\subseteq a'k). \]
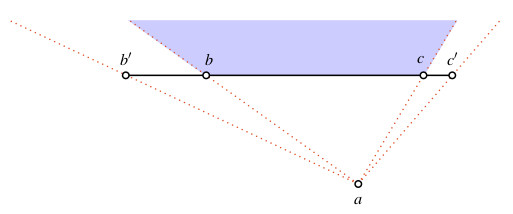
Sind \( a \) ein beliebiger Punkt und \( h \) und \( k \) zwei geometrische Figuren, wobei \( h \) in \( k \) enthalten ist, so ist auch \( a'h \) in \( a'k \) enthalten.
| Beweis: | ||
|
Nach Voraussetzung ist \( h\subseteq k \). |
||
|
1. |
Falls \( y\in h, \) so ist \( y\in k \) |
(Vor) |
|
Es sei \( z\in a'h \) beliebig. Wir zeigen \( z\in a'k. \) |
||
|
2. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\ \mbox{mit}\ x\in a'y\} \) |
(Def 4) |
|
3. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in a'y\} \) |
(1, 2) |
|
4. |
Es ist \( z\in a'k \) |
(3, Def 4) |
|
Damit ist der Beweis abgeschlossen. \( \quad\Box \) |
||
Es seien \( a\in{\mathcal P} \) und \( h,k\in{\mathcal F}. \) Dann gilt \[ (h\subseteq k)\longrightarrow(ah'\subseteq ak'). \]

Sind \( a \) ein beliebiger Punkt und \( h \) und \( k \) zwei geometrische Figuren, wobei \( h \) in \( k \) enthalten ist, so ist auch \( ah' \) in \( ak' \) enthalten.
| Beweis: | ||
|
Nach Voraussetzung ist \( h\subseteq k \). |
||
|
1. |
Falls \( y\in h, \) so ist \( y\in k \) |
(Vor) |
|
Es sei \( z\in ah' \) beliebig. Wir zeigen \( z\in ak'.\) |
||
|
2. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\ \mbox{mit}\ x\in ay'\} \) |
(Def 5) |
|
3. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in ay'\} \) |
(1, 2) |
|
4. |
Es ist \( z\in ak' \) |
(3, Def 5) |
|
Damit ist der Beweis abgeschlossen. \( \quad\Box \) |
||
Es seien \( a\in{\mathcal P} \) und \( h,k\in{\mathcal F}. \) Dann gilt \[ a(h\cup k)=ah\cup ak. \]
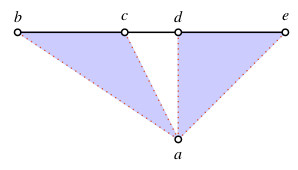
|
Beweis: |
||
|
Es sei \( z\in a(h\cup k). \) Wir zeigen \( z\in ah\cup ak. \) |
||
|
1. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\cup k\ \mbox{mit}\ x\in ay\} \) |
(Def 3) |
|
2. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\ \mbox{mit}\ x\in ay\} \) |
|
|
|
oder \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in ay\} \) |
(1) |
|
3. |
Es ist \( z\in ah \) oder \( z\in ak \) |
(2, Def 3) |
|
4. |
Es ist \( z\in ah\cup ak \) |
(3) |
|
Es sei \( z\in ah\cup ak. \) Wir zeigen \( z\in a(h\cup k). \) |
||
|
5. |
Es ist \( z\in ah \) oder \( z\in ak \) |
|
|
6. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\ \mbox{mit}\ x\in ay\} \) |
|
|
|
oder \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in ay\} \) |
(5, Def 3) |
|
7. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\cup k\ \mbox{mit}\ x\in ay\} \) |
(6) |
|
8. |
Es ist \( z\in a(h\cup k) \) |
(7, Def 3) |
|
Damit ist der Beweis abgeschlossen. \( \quad\Box \) |
||
Es seien \( a\in{\mathcal P} \) und \( h,k\in{\mathcal F}. \) Dann gilt \[ a'(h\cup k)=a'h\cup a'k. \]
| Beweis: | ||
|
Es sei \( z\in a'(h\cup k). \) Wir zeigen \( z\in a'h\cup a'k. \) |
||
|
1. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\cup k\ \mbox{mit}\ x\in a'y\} \) |
(Def 4) |
|
2. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\ \mbox{mit}\ x\in a'y\} \) |
|
|
|
oder \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in a'y\} \) |
(1) |
|
3. |
Es ist \( z\in a'h \) oder \( z\in a'k \) |
(2, Def 4) |
|
4. |
Es ist \( z\in a'h\cup a'k \) |
(3) |
|
Es sei \( z\in a'h\cup a'k. \) Wir zeigen \( z\in a'(h\cup k). \) |
||
|
5. |
Es ist \( z\in a'h \) oder \( z\in a'k \) |
|
|
6. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\ \mbox{mit}\ x\in a'y\} \) |
|
|
|
oder \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in a'y\} \) |
(5, Def 3) |
|
7. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\cup k\ \mbox{mit}\ x\in a'y\} \) |
(6) |
|
8. |
Es ist \( z\in a'(h\cup k) \) |
(7, Def 4) |
|
Damit ist der Beweis abgeschlossen. \( \quad\Box \) |
||
Es seien \( a\in{\mathcal P} \) und \( h,k\in{\mathcal F}. \) Dann gilt \[ a(h\cup k)'=ah'\cup ak'\,. \]
| Beweis: | ||
|
Es sei \( z\in a(h\cup k)'. \) Wir zeigen \( z\in ah'\cup ak'. \) |
||
|
1. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\cup k\ \mbox{mit}\ x\in ay'\} \) |
(Def 5) |
|
2. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\ \mbox{mit}\ x\in ay'\} \) |
|
|
|
oder \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in ay'\} \) |
(1) |
|
3. |
Es ist \( z\in ah' \) oder \( z\in ak' \) |
(2, Def 5) |
|
4. |
Es ist \( z\in ah'\cup ak' \) |
(3) |
|
Es sei \( z\in ah'\cup ak'. \) Wir zeigen \( z\in a(h\cup k)'. \) |
||
|
5. |
Es ist \( z\in ah' \) oder \( z\in ak' \) |
|
|
6. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\ \mbox{mit}\ x\in ay'\} \) |
|
|
|
oder \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in ay'\} \) |
(5, Def 5) |
|
7. |
Es ist \( z\in\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in h\cup k\ \mbox{mit}\ x\in ay'\} \) |
(6) |
|
8. |
Es ist \( z\in a(h\cup k)' \) |
(7, Def 5) |
|
Damit ist der Beweis abgeschlossen. \( \quad\Box \) |
||
Es seien \( a\in{\mathcal P} \) und \( k\in{\mathcal F} \) mit \( k=\emptyset. \) Dann gelten \[ ak=\emptyset\quad\mbox{und}\quad a'k=\emptyset\quad\mbox{und}\quad ak'=\emptyset\,. \]
Beweis: Wir beweisen nur die erste Aussage. Existiert nämlich ein \( z\in{\mathcal P} \)
mit
\[ z\in ak=\{x\in{\mathcal P}\,:\,\mbox{es gibt ein}\ y\in k\ \mbox{mit}\ x\in ay\}, \]
so existiert auch ein \( y\in k \) mit \( z\in ay. \) Es ist aber nach Voraussetzung \( k=\emptyset. \) Widerspruch. \( \quad\Box \)