Buch I

EUKLIDS ELEMENTE BUCH I

Aufbau des ersten Buches

Das erste Buch der Elemente besteht aus 23 Definitionen, 6 Postulaten, 8 Axiomen und 48 Propositionen:

Definitionen
Postulate
Axiome
Propositionen

Verwendete Literatur

Für unsere Darstellung der Definitionen, Postulate, Axiome und Propositionen haben wir folgende Ausgaben als Grundlage herangezogen:

Heiberg, J.L.: Euclidis Opera Omnia I (Teubner, 1883)
Heath, T.L.: The thirteen books of Euclid's elements I (The University Press, 1908)
Simon, M.: Euclid und die sechs planimetrischen Bücher (Teubner, 1901)
Steck, M.: Proklus Diadochus. Euklidkommentar (Kais. Leop.-Carol. Dt. Akad. d. Naturf., 1945)
Thaer, C.: Die Elemente. (Wissenschaftliche Buchgesellschaft Darmstadt, 1969)

Definitionen

Bedeutung der Definitionen

Den Postulaten, Axiomen und Propositionen des ersten Buches der Elemente gehen 23 explizite Definitionen voraus. In späteren Untersuchungen wird auf sie eventuell nicht zurückgegriffen, für ein

umfassendes Verständnis der Geometrie Euklids sind sie jedoch unverzichtbar.

Zu den Definition fügen wir zusätzliche Quellenstudien hinzu:

Darstellung der Definitionen

Definition I.1
Ein Punkt ist, dessen Teil nichts ist.
Dieser Definition fügen wir hier ein Quellenstudium hinzu.

Definition I.2
Eine Linie ist breitenlose Länge.
Dieser Definition fügen wir hier ein Quellenstudium hinzu.

Definition I.3
Die Enden einer Linie sind Punkte.

Definition I.4
Eine gerade Linie ist eine Linie, die zu den Punkten an ihr gleichmäßig liegt.

Definition I.5
Eine Fläche ist das, was nur Länge und Breite hat.

Definition I.6
Die Enden einer Fläche sind Linien.

Definition I.7
Eine ebene Fläche ist eine Fläche, wenn zu den sie begrenzenden geraden Linien gleichmäßig liegt.

Definition I.8
Ein ebener Winkel ist die Neigung zweier Linien in einer Ebene, welche sich schneiden und nicht in einer geraden Linie liegen.

Definition I.9
Wenn die Linien, die den Winkel umfassen, gerade Linien sind, heißt der Winkel geradlinig.

Definition I.10
Wenn eine gerade Linie, auf eine gerade Linie gestellt, zwei gleiche benachbarte Winkel bildet, dann ist jeder der beiden gleichen Winkel ein rechter Winkel, und die aufgestellte gerade Linie heißt senkrecht zu der, auf der sie steht.

Definition I.11
Ein stumpfer Winkel ist ein Winkel, der größer als ein rechter Winkel ist.

Definition I.12
Ein spitzer Winkel ist ein Winkel, der kleiner als ein rechter Winkel ist.

Definition I.13
Eine Grenze ist das, was das Äußerste von irgendetwas ist.

Definition I.14
Eine Figur ist das, was von einer Grenze oder von Grenzen umfasst wird.

Definition I.15
Ein Kreis ist eine ebene Figur, die von einer Linie umfasst wird (die Peripherie heißt), so dass alle geraden Linien, die von einem innerhalb der Figur liegenden Punkt bis zur Linie (zur Peripherie des Kreises) verlaufen, einander gleich sind.

Definition I.16

Und dieser Punkt heißt Mittelpunkt des Kreises.

Definition I.17
Ein Durchmesser des Kreises ist eine beliebige gerade Linie, die durch den Mittelpunkt verläuft und in beiden Richtungen vom Umfang des Kreises begrenzt wird; und eine solche gerade Linie halbiert auch den Kreis.

Definition I.18
Ein Halbkreis ist eine Figur, die vom Durchmesser und dem von ihm abgeschnittenen Umfang begrenzt wird. Und der Mittelpunkt des Halbkreises ist der derselbe wie der vom Kreis.

Definition I.19
Geradlinige Figuren sind solche, welche von geraden Linien umfasst werden; dreiseitige Figuren sind dabei solche, die umfasst werden von drei; vierseitige solche, die umfasst werden von vier; und vielseitige solche, die umfasst werden von mehr als vier geraden Linien.

Definition I.20
Von den dreiseitigen Figuren ist ein gleichseitiges Dreieck das, welches drei gleiche Seiten hat; ein gleichschenkliges Dreieck das, welches zwei gleiche Seiten hat; und ein ungleichseitiges Dreieck das, welches drei ungleiche Seiten hat.

Definition I.21
Weiter ist von den dreiseitigen Figuren ein rechtwinkliges Dreieck das, welches einen rechten Winkel hat; ein stumpfwinkliges Dreieck das, welches einen stumpfen Winkel hat; und ein spitzwinkliges Dreieck das, welches drei spitze Winkel hat.

Definition I.22
Von den vierseitigen Figuren ist ein Quadrat das, welches gleichseitig und rechtwinklig ist; ein längliches Rechteck das, welches rechtwinklig, aber nicht gleichseitig ist; ein Rhombus das, welche gleichseitig, aber nicht rechtwinklig ist; und ein Rhomboid das, in welchem die entgegengesetzten Seiten und Winkel gleich sind, aber das weder gleichseitig noch rechtwinklig ist.

Definition I.23
Parallele gerade Linien sind gerade Linien, welche in einer Ebene liegen und, wenn in beiden Richtungen unbegrenzt fortgesetzt, sich in keiner Richtung schneiden.

Postulate

Bedeutung der Postulate

Die Euklidischen Postulate stellen geometrische Aussagen dar, welche uneingeschränkt und ohne jede Zweifel akzeptiert werden sollen und daher keiner eigenen Beweise bedürfen. Wir können sie als semantische Wahrheiten der Elemente verstehen.

Das sechste Postulat I.6 wurde den Elementen in späterer Zeit zum Zweck des Beweises des Parallelenpostulats hinzugefügt. Es erscheint in vergleichbarer Form in C. Thaer als neuntes Axiom; auf Grund seines rein geometrischen Inhalts fügen wir es in unseren Text als Postulat ein.

Darstellung der Postulate

Postulat I.1
Das Folgende sei gefordert: Eine gerade Linie lasse sich von einem beliebigen Punkt zu einem beliebigen Punkt ziehen.

Postulat I.2
Eine endliche gerade Linie lasse sich zusammenhängend zu einer geraden Linie verlängern.

Postulat I.3
Zu jedem Mittelpunkt und jedem Abstand lasse sich der Kreis beschreiben.

Postulat I.4
Alle rechten Winkel sind einander gleich.

Postulat I.5
Wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass die innen auf derselben Seite liegenden Winkel zusammen kleiner als zwei rechte Winkel werden, so treffen sich die beiden geraden Linien, falls unbegrenzt fortgesetzt, auf der Seite, auf welcher die Winkel liegen, die zusammen kleiner als zwei rechte Winkel sind.

Postulat I.6
Zwei gerade Linien umfassen keine Fläche.

Axiome

Bedeutung der Axiome

Den Postulaten schließen sich acht Axiome logischen bzw. arithmetischen Inhalts an. Wir können sie als syntaktische Wahrheiten der Elemente verstehen.

Gewöhnlich wird das obige sechste Postulat, welches rein geometrischen Inhalts ist und den Elementen erst später zum Zwecke des Beweises des Parallelenpostulats hinzugefügt wurde, als neuntes Axiom aufgeführt.

Darstellung der Axiome

Axiom I.1

Dinge, die demselben gleich sind, sind auch einander gleich.

Arithmetische Interpretation: $ (a=c)\wedge(b=c)\longrightarrow(a=b) $

Axiom I.2

Wenn Gleiche zu Gleichen addiert werden, so sind die Ganzen gleich.

Arithmetische Interpretation: $ (a=b)\wedge(c=d)\longrightarrow(a+c=b+d) $

Axiom I.3

Wenn Gleiche von Gleichen weggenommen werden, so sind die Reste gleich.

Arithmetische Interpretation: $ (a=b)\wedge(c=d)\longrightarrow(a-c=b-d) $

Axiom I.4

Wenn Gleiche zu Ungleichen addiert werden, so sind die Ganzen ungleich.

Arithmetische Interpretation: $ (a=b)\wedge(c\not=d)\longrightarrow(a+c\not=b+d) $

Axiom I.5

Dinge, die das Doppelte von demselben sind, sind einander gleich.

Arithmetische Interpretation: $ (a=2c)\wedge(b=2c)\longrightarrow(a=b) $

Axiom I.6

Dinge, die die Hälfte von demselben sind, sind einander gleich.

Arithmetische Interpretation: $ \displaystyle\left(a=\frac{c}{2}\right)\wedge\left(b=\frac{c}{2}\right)\longrightarrow(a=b) $

Axiom I.7

Dinge, die sich decken, sind einander gleich.

Axiom I.8

Das Ganze ist größer als sein Teil.

Propositionen (I.1 bis I.30)

Bedeutung der Propositionen

Die Propositionen des ersten Buches der Elemente enthalten grundlegende Aussagen der ebenen Geometrie der geraden Linien, paralleler Linien, Dreiecke, Vierecke, Parallelogramme.

Einteilung der Propositionen

Nach T.L. Heath lassen sich die Proposition in drei Gruppen einteilen:

Propositionen I.1 bis I.26:

Sätze über Dreiecke, sich schneidende Geraden, aufeinander senkrecht stehende Geraden usw. ohne Berücksichtigung des Parallelenpostulats

Propositionen I.27 bis I.32

Sätze über Parallelen unter Berücksichtigung des Parallelenpostulats

Propositionen I.33 bis I.48

Sätze über Dreiecke, Vierecke, Parallelogramme usw. mit Berücksichtigung ihrer Inhalte

Inhaltlich können wir sie so zusammenfassen:

Konstruktion eines gleichseitigen Dreiecks
Abtragung einer Strecke an einem Punkt
Abtragung einer kürzeren auf einer längeren Strecke
Kongruenzsatz SWS für Dreiecke
Gleichheit der Basiswinkel im gleichschenkligen Dreieck
...
...
Kongruenzsatz SSS für Dreiecke
Halbierung eines Winkels
Halbierung einer Strecke
Konstruktion des Lots
...
Nebenwinkel bilden zusammen zwei Rechte
...
Gleichheit der Scheitelwinkel
...
...
...
...
...
...
...
...
...
...
Kongruenzsatz WSW für Dreiecke
...
Umkehrung des Parallelenpostulats
...
Transzendens der Parallelität
Vorbereitung zu Playfairs Parallelenpostulats
Innenwinkelsatz für Dreiecke
...
...
...
...
...
...
...
...
...
...
...
...
...
Konstruktion des Quadrats über einer Strecke
Satz des Pythagoras
Umkehrung des Satzes von Pythagoras

Zu den Propositionen führen wir zusätzliche Kommentare hinzu:

Kommentare zu Proposition I.4

Darstellung der Propositionen

Proposition I.1 (Konstruktionsaufgabe)

Auf einer gegebenen endlichen geraden Linie ist ein gleichseitiges Dreieck zu konstruieren.

$ABC$ $ABC$ $ABC$ $ABC$

Konstruktion
Aufgabenstellung
$ AB $ sei die vorgelegte Gerade, über der ein gleichseitiges Dreieck errichtet werden soll
Vorbereitende Konstruktion
1.	Konstruiere den Kreis mit Mittelpunkt $ A $ und Abstand $ AB $	(Post I.3)
2.	Konstruiere den Kreis mit Mittelpunkt $ B $ und Abstand $ AB $	(Post I.3)
Zwischenschritt
3.	Beide Kreise schneiden sich in einem Punkt $ C $	(Disk)
Abschluss der Konstruktion
4.	Konstruiere von $ A $ nach $ C $ die gerade Linie $ AC $	(Post I.1)
5.	Konstruiere von $ B $ nach $ C $ die gerade Linie $ BC $	(Post I.1)
Beweis, dass $ ABC $ gleichseitig ist
6.	$ \vdash\ AC = AB $	(1, Def I.15)
7.	$ \vdash\ BC = AB $	(2, Def I.15)
8.	$ \vdash\ AC = BC $	(6, 7, Ax I.1)
Damit ist die Konstruktion abgeschlossen. $ \quad\Box $

Diskussion

Im dritten Schritt wird behauptet, dass sich die beiden vorher konstruierten Kreise in einem Punkt $ C $ schneiden. Das bedarf einer Erläuterung:

Interpretieren wir Proposition I.1 als Konstruktionsaufgabe in der Euklidischen Ebene, wie von uns auch dargestellt, so ist nichts zu beweisen. Die Existenz des in Frage stehenden Schnittpunkts wird einfach unterstellt. Überhaupt können nur solche geometrischen Objekte konstruiert werden, die auch existieren.
Interpretieren wir in Proposition I.1 eine Existenzsaussage hinein, so fehlt ein Argument.

Die moderne axiomatische Geometrie setzt zur Sicherung der Existenz eines solchen Schnittpunkts Axiome der folgenden Art an den Beginn der Theorie:

Axiom über die Existenz eines Schnittpunkts zwischen Linie und Kreis,
Axiom über die Existenz zweier Schnittpunkte zwischen zwei Kreisen,
Stetigkeitsaxiome.

Es war wohl Leibniz, der als Erster auf diesen kritischen Punkt in der Konstruktion aufmerksam machte.

Proposition I.2 (Konstruktionsaufgabe)
An einen gegebenen Punkt eine einer gegebenen geraden Linie gleiche gerade Linie anzulegen.

Aufgabenstellung
$ AB $ sei die vorgelegte gerade Linie, die am Punkt $ A $ angelegt werden soll
Vorbereitende Konstruktion
1.	Konstruiere von $ A $ nach $ B $ die gerade Linie $ AB $	(Post I.1)
2.	Konstruiere von über $ AB $ das gleichseitige Dreieck $ ABD $	(Prop I.1)
3.	Verlängere die gerade Linie $ AD $ zur geraden Linie $ DE $	(Post I.2)
4.	Verlängere die gerade Linie $ BD $ zur geraden Linie $ DF $	(Post I.2)
5.	Konstruiere den Kreis mit Mittelpunkt $ B $ und Abstand $ BC $	(Post I.3)
Erster Zwischenschritt
6.	Die gerade Linie $ DF $ schneidet diesen Kreis im Punkt $ G $
Abschluss der Konstruktion
7.	Konstruiere den Kreis mit Mittelpunkt $ D $ und Abstand $ DG $	(Post I.3)
Zweiter Zwischenschritt
8.	Die gerade Linie $ DE $ schneidet diesen Kreis im Punkt $ L $
Beweis, dass es sich bei $ AL $ um die gesuchte gerade Linie handelt
9.	Es ist $ BC = BG $	(5, 6, Def I.15)
10.	Es ist $ DG = DL $	(7, 8, Def I.15)
11.	Es ist $ AD = BD $	(1, 2, Def I.20)
12.	Es ist $ BD + BG = DG $	(4, 6)
13.	Es ist $ AD + BG = DG $	(11, 12, Ax I.1)
14.	Es ist $ AD + AL = DL $	(3, 8)
15.	Es ist $ AD + AL = DG $	(10, 14, Ax I.1)
16.	Es ist $ AL = BG $	(13, 15, Ax I.3)
17.	Es ist $ AL = BC $	(9, 16, Ax I.1)
Damit ist die Konstruktion abgeschlossen. $ \quad\Box $

Diskussion

Im sechsten und im achten Beweisschritt werden die Existenz der Schnittpunkte $ G $ und $ L $ behauptet. Unsere Kritik zur Beweisführung von Proposition I.1 ist also auch hier angebracht: Dort handelte es sich um die Existenz des Schnittpunktes zweier gewisser Kreise, hier eines Kreises und einer Geraden.

Proposition I.3

Wenn zwei ungleiche gerade Linien gegeben sind, von der größeren eine der kleineren gleiche gerade Linie abzutragen.

Diskussion

...

Proposition I.4 (Lehrsatz)

Wenn in zwei Dreiecken zwei Seiten zwei Seiten entsprechend gleich sind, und wenn die von den gleichen Seiten eingeschlossenen Winkel einander gleich sind, so ist die Grundseite der Grundseite entsprechend gleich, das Dreieck ist dem Dreieck gleich, und die übrigen Winkel sind den übrigen Winkeln entsprechend gleich, nämlich solche, denen gleiche Seiten gegenüberliegen.

Aufgabenstellung
Gegeben sind $ AC=DF, $ $ AB=DE $ und $ \angle(CAB)=\angle(DFE). $ Zu zeigen sind $ ABC=DEF $ sowie $ \angle(ABC)=\angle(DEF) $ und $ \angle(BCA)=\angle(EFD). $
Vorbereitende Konstruktion
1.	Verschiebe das Dreieck $ ABC $ auf das Dreieck $ DEF $
Erster Zwischenschritt
2.	Es ist $ A=D $	(1)
3.	Es ist $ AB=DE $	(1)
Zweiter Zwischenschritt
4.	Es ist $ B=E $	(2, 3)
5.	Es ist $ AC=DF $	(Vor, 3)
6.	Es ist $ C=F $	(5)
7.	Es ist $ B=E $	(3)
8.	Es ist $ BC=EF $	(6, 7, Post I.6)
Abschluss des Beweises
9.	Es ist $ ABC=DEF $	(3, 5, 8)
10.	Es ist $ \angle(ABC)=\angle(DEF) $	(9)
11.	Es ist $ \angle(BCA)=\angle(EFD) $	(9)
Damit ist der Beweis abgeschlossen. $ \quad\Box $

Diskussion

Ein Dreieck ist eine dreiseitige Figur, die nach Definition I.19 durch drei Seiten eindeutig gegeben ist. Der wesentliche Kritikpunkt des vorgelegten Beweises ist dann das Verschieben des Dreiecks $ ABC $ bzw. das Übereinanderlegen der Dreiecke $ ABC $ und $ DEF. $ Geometrische Operationen dieser Art (Kongruenzoperationen) sind aber in den Euklidischen Postulaten bzw. Axiomen nicht vorgesehen.

Dieser Diskussion fügen wir hier historische Kommentare hinzu.

Proposition I.5 (Lehrsatz)

Im gleichschenkligen Dreieck sind die Winkel an der Grundlinie einander gleich, und werden die anderen beiden, gleichen Seiten verlängert, so sind auch die Winkel unterhalb der Grundlinie einander gleich.

Aufgabenstellung
Gegeben ist das gleichschenklige Dreieck $ ABC $ mit $ AB=AC. $Zu zeigen sind $ \angle(ABC)=\angle(BCA) $ und $ \angle(CBD)=\angle(ECB). $
Vorbereitende Konstruktion
1.	Verlängere die gerade Linie $ AB $ zur geraden Linie $ AD $	(Post I.2)
2.	Verlängere die gerade Linie $ AC $ zur geraden Linie $ AE $	(Post I.2)
3.	Wähle auf $ BD $ einen Punkt Punkt $ F $ beliebig	(Def I.4)
4.	Trage auf $ AE $ die kürzere gerade Linie $ AG=AF $ ab	(Prop I.3)
5.	Konstruiere von $ C $ nach $ F $ die gerade Linie $ CF $	(Post I.1)
6.	Konstruiere von $ B $ nach $ G $ die gerade Linie $ BG $	(Post I.1)
Erster Zwischenschritt
7.	Es ist $ AF=AG $	(4)
8.	Es ist $ \angle(AF,AG)=\angle(AB,AC) $	(1, 2, 3, 4)
9.	Es ist $ \angle(AB,AC)=\angle(GAF) $
10.	Es ist $ CF=BG $	(7, 8, 9, Prop I.4)
11.	Es ist $ ACF=ABG $	(7, 8, 9, Prop I.4)
12.	Es ist $ \angle(FCA)=\angle(ABG) $	(7, 8, 9, Prop I.4)
13.	Es ist $ \angle(AGB)=\angle(AFC) $	(7, 8, 9, Prop I.4)
Zweiter Zwischenschritt
14.	Es ist $ BF=CG $	(7, Ax I.3)
15.	Es ist $ \angle(BFC)=\angle(BGC) $	(13)
16.	Es ist $ BCF=BCG $	(10, 14, 15, Prop I.4)
17.	Es ist $ \angle(CBF)=\angle(GCB) $	(10, 14, 15, Prop I.4)
18.	Es ist $ \angle(FCB)=\angle(CBG) $	(10, 14, 15, Prop I.4)
Abschluss des Beweis
19.	Es ist $ \angle(ABG)=\angle(ABC)+\angle(CBG) $
20.	Es ist $ \angle(FCA)=\angle(ABC)+\angle(FCB) $	(12, 18)
21.	Es ist $ \angle(FCA)=\angle(BCA)+\angle(FCB) $
22.	Es ist $ \angle(ABC)=\angle(BCA) $	(20, 21, Ax I.3)
23.	Es ist $ \angle(CBF)=\angle(CBD) $
24.	Es ist $ \angle(GCB)=\angle(CBD) $	(17, 23)
25.	Es ist $ \angle(ECB)=\angle(GCB) $
26.	Es ist $ \angle(CBD)=\angle(ECB) $	(24, 25, Ax I.1)
Damit ist der Beweis abgeschlossen. $ \quad\Box $

Diskussion

...

Proposition I.6 (Lehrsatz)

Wenn in einem Dreieck zwei Winkel einander gleich sind, so sind auch die Seiten, die den gleichen Winkeln gegenüberliegen, einander gleich sein.

Diskussion

...

Proposition I.7 (Lehrsatz)

Werden an den Enden einer gegebenen geraden Linie zwei gerade Linien angesetzt, die sich in einem Punkt schneiden, so ist es nicht möglich, auf derselben Seite und an den Enden der gegebenen geraden Linie zwei weitere gerade Linien anzusetzen, die den beiden ersten geraden Linien entsprechend gleich sind, sich aber in einem anderen Punkt schneiden.

Diskussion

...

Proposition I.8 (Lehrsatz)

Wenn in zwei Dreiecken zwei Seiten zwei Seiten entsprechend gleich sind, und wenn auch die eine Grundlinie der anderen Grundlinie gleich ist, so sind die von den gleichen Seiten eingeschlossenen Winkel gleich.

Diskussion

...

Proposition I.9 (Konstruktionsaufgabe)

Einen gegebenen geradlinigen Winkel zu halbieren.

Diskussion

...

Proposition I.10 (Konstruktionsaufgabe)

Eine gegebene gerade Linie zu halbieren.

Diskussion

...

Proposition I.11 (Konstruktionsaufgabe)

Auf einer gegebenen geraden Linie und von einem auf dieser Linie gegebenen Punkt aus rechtwinklig eine gerade Linie zu ziehen.

Diskussion

...

Proposition I.12 (Konstruktionsaufgabe)

Auf eine gegebene, unbegrenzte gerade Linie von einem nicht auf ihr gelegenen Punkt aus das Lot zu fällen.

Diskussion

...

Proposition I.13 (Lehrsatz)

Wird eine gerade Linie auf eine weitere gerade Linie gestellt, und bilden diese beiden geraden Linien zwei Winkel, so sind diese entweder zwei Rechte sind, oder sind zusammen zwei Rechten gleich.

Diskussion

...

Proposition I.14 (Lehrsatz)

Bilden an einer gegebenen geraden Linie in einem auf gelegenen Punkt zwei nicht auf derselben Seite liegende weitere zwei gerade Linien benachbarte Winkel, die zusammen gleich zwei Rechten sind, so setzen sich diese zwei geraden Linien einander gerade fort.

Diskussion

...

Proposition I.15 (Lehrsatz)

Wenn sich zwei gerade Linien schneiden, so sind die dabei entstehenden, senkrecht gegenüberliegenden Winkel gleich.

Diskussion

...

Proposition I.16 (Lehrsatz)

Wird in einem Dreieck eine Seite verlängert, so ist der dabei entstehende äußere Winkel größer als jeder der beiden gegenüberliegenden inneren Winkel.

Diskussion

...

Proposition I.17 (Lehrsatz)

In jedem Dreieck sind zwei beliebige Winkel zusammen genommen kleiner als zwei Rechte.

Diskussion

...

Proposition I.18 (Lehrsatz)

In jedem Dreieck liegt der größeren Seite der größere Winkel gegenüber.

Diskussion

...

Proposition I.19 (Lehrsatz)

In jedem Dreieck liegt dem größeren Winkel die größere Seite gegenüber.

Diskussion

...

Proposition I.20 (Lehrsatz)

In jedem Dreieck sind zwei Seiten, beliebig zusammengenommen, größer als die dritte.

Diskussion

...

Proposition I.21 (Lehrsatz)

Diskussion

...

Proposition I.22 (Konstruktionsaufgabe)

Diskussion

...

Proposition I.23 (Konstruktionsaufgabe)

Diskussion

...

Proposition I.24 (Lehrsatz)

Diskussion

...

Proposition I.25 (Lehrsatz)

Diskussion

...

Proposition I.26 (Lehrsatz)

Diskussion

...

Proposition I.27 (Lehrsatz)

Diskussion

...

Proposition I.28 (Lehrsatz)

Diskussion

...

Proposition I.29 (Lehrsatz)

Diskussion

...

Proposition I.30 (Lehrsatz)

Diskussion

...

Proposition I.43 (Lehrsatz)

In einem Parallelogramm sind die Ergänzungen der um die Diagonale liegenden Parallelogramme einander gleich.

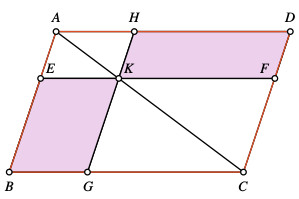
Aufgabenstellung
$ ABCD $ sei das vorgelegte Parallelogramm. Die Diagonale $ AC $ und ein Punkt $ K $ auf ihr erzeugen die Parallelogramme $ EKHA $ und $ GCFK. $ Zu zeigen ist $ \|BGKE\| = \|KFDH\|. $
Vorbereitende Konstruktion
1.	Konstruiere durch $ K $ die zu $ AB $ parallele gerade Linie	(Prop I.31)
2.	Konstruiere durch $ K $ die zu $ BC $ parallele gerade Linie	(Prop I.31)
Erster Zwischenschritt
3.	Die Parallele aus (1) schneidet $ BC $ im Punkt $ G $
4.	Die Parallele aus (1) schneidet $ AD $ im Punkt $ H $
5.	Die Parallele aus (2) schneidet $ AB $ im Punkt $ E $
6.	Die Parallele aus (2) schneidet $ CD $ im Punkt $ F $
Zweiter Zwischenschritt
7.	Es ist $ EKHA $ ein Parallelogramm	(1, 2)
8.	Es ist $ GCFK $ ein Parallelogramm	(1, 2)
Dritter Zwischenschritt
9.	Es ist $ ABC = ACD $	(Prop I.34)
10.	Es ist $ AEK = AKH $	(7, Prop I.34)
11.	Es ist $ GCK = CFK $	(8, Prop I.34)
Vierter Zwischenschritt
12.	Es ist $ \|ABC\| = \|ACD\| $	(9)
13.	Es ist $ \|AEK\| = \|AKH\| $	(10)
14.	Es ist $ \|GCK\| = \|CFK\| $	(11)
Fünfter Zwischenschritt
15.	Es ist $ \|AEK\|+\|GCK\|=\|AKH\|+\|GCK\| $	(13, Ax I.2)
16.	Es ist $ \|GCK\|+\|AKH\|=\|CFK\|+\|AKH\| $	(14, Ax I.2)
17.	Es ist $ \|AEK\|+\|GCK\|=\|CFK\|+\|AKH\| $	(15, 16, Ax I.1)
Sechster Zwischenschritt
18.	Es ist $ \|ABC\|=\|AEK\|+\|GCK\|+\|BGKE\| $
19.	Es ist $ \|ACD\|=\|AKH\|+\|CFK\|+\|FDHK\| $
Abschluss des Beweises
20.	Es ist $\|AEK\|+\|GCK\|+\|BGKE\|=\|AKH\|+\|CFK\|+\|FDHK\|$	(18, 19, Ax I.1)
21.	Es ist $\|AEK\|+\|GCK\|+\|BGKE\|=\|AEK\|+\|GCK\|+\|FDHK\|$	(17, 20, Ax I.2)
22.	Es ist $\|BGKE\|=\|FDHK\|$	(21, Ax I.3)
Damit ist der Beweis abgeschlossen. $ \quad\Box $

Diskussion

...

Fortsetzung Propositionen I.31 bis I.48