EPITROCHOIDS
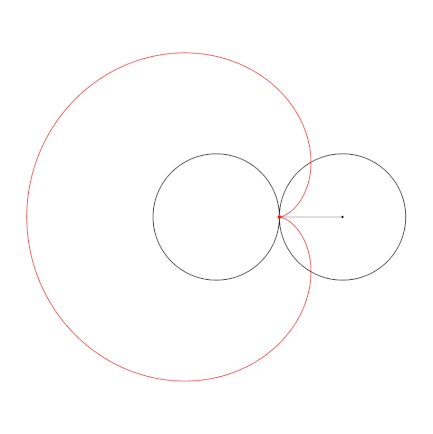
Radius of the inner circle: 2.5
Radius of the rolling circle: 2.5
Point distance to rolling centre: 2.5
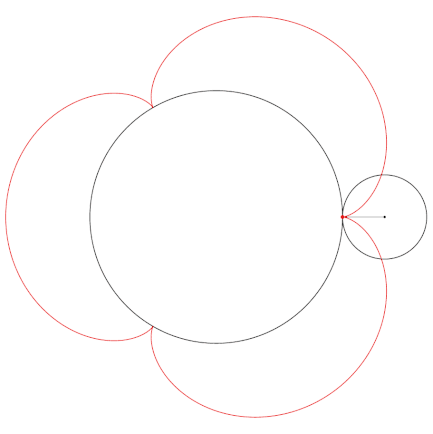
Radius of the inner circle: 4.0
Radius of the rolling circle: 2.0
Point distance to the rolling centre: 2.0

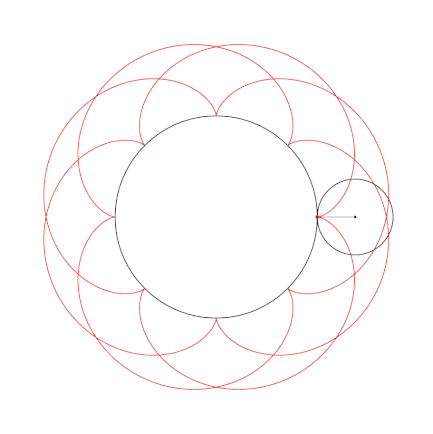
Radius of the inner circle: 5.0
Radius of the rolling circle: 1.66
Point distance to the rolling centre: 1.66
Radius of the inner circle: 4.0
Radius of the rolling circle: 1.5
Point distance to the rolling centre: 1.5
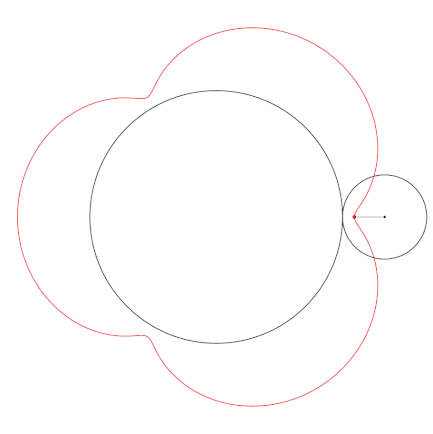
Radius of the inner circle: 5.0
Radius of the rolling circle: 1.66
Point distance to the rolling centre: 1.2
Epitrochoid
Epitrochoid (point at distance \( d \) on a circle of radius \( r \) rolling outside a fixed circle of radius \( R \))
$$ x(\theta) = (R+r)\cos(\theta) - d\cos\!\left(\frac{R+r}{r}\,\theta\right),\qquad y(\theta) = (R+r)\sin(\theta) - d\sin\!\left(\frac{R+r}{r}\,\theta\right). $$Special case (epicycloid, \( d=r \))
$$ x(\theta) = (R+r)\cos(\theta) - r\cos\!\left(\frac{R+r}{r}\,\theta\right),\qquad y(\theta) = (R+r)\sin(\theta) - r\sin\!\left(\frac{R+r}{r}\,\theta\right). $$- Mouse wheel: zoom
Created by Yannick Häberlin with WebGL (part of his Bachelor thesis)