Hausaufgabenblatt 4
Aufgabe HA 13
Es sei \( \mathbb K \) ein angeordneter Körper. Beweisen Sie:
| (i) | Dreiecksungleichung |
\[ |x+y|\le|x|+|y|\quad\mbox{für alle}\ x,y\in\mathbb K \]
| (ii) | inverse Dreiecksungleichung |
\[ \big||x|-|y|\big|\le|x-y|\quad\mbox{für alle}\ x,y\in\mathbb K. \]
Lösung
Aufgabe HA 14
Beweisen Sie, dass folgende Zahlen nicht rational sind.
| (i) | \( \sqrt{2}+\sqrt{6} \) |
| (ii) | \( \sqrt{2}+\sqrt{3} \) |
Lösung
Aufgabe HA 15
Wie in Präsenzaufgabe 17, jetzt aber für die folgende Skizze
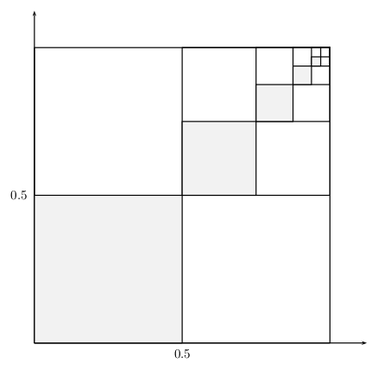
Lösung
Aufgabe HA 16
Betrachten Sie den folgenden rekursiven Konstruktionsprozess:
| 1. | Beginne mit einer geraden Strecke der Länge \( 1 \) (Menge \( C_0 \)). |
| 2. | Lösche das mittlere Drittel von \( C_0 \) (ohne die beiden Randpunkte links und rechts dieses mittleren Drittels; Ergebnis ist die Menge \( C_1 \)). |
| 3. | Lösche die mittleren Drittel von \( C_1 \) (ohne die linken und rechten Randpunkte des Geöschten; Ergebnis ist die Menge \( C_2 \)) usw. |
Die Cantorsche Mittel-Drittel-Menge \( C\subset\mathbb R \) ist dann definiert als der Durchschnitt \[ C:=\bigcap_{k=0}^\infty C_k\,. \] Welche Länge besitzen \( C_0, \) \( C_1, \) \( C_2 \) usw. sowie \( C \) selbst?
Lösung
